[ answers in web view ]
Name: _______________________________ K E Y
Student ID: _______________________________

Total points: 50
  1. Describe the five hardware abstractions mentioned in the text. [5]

    _Input__________ _Storage__________ _Processing__________ _Control__________ _Output__________
  2. Name the five steps to top-down problem solving as described in the text. (It's okay if you can't remember the exact wording; the concepts are more important.) [5]
    _Write__________ _Apprehend__________ _Design__________ _Execute__________ _Scrutinize__________
  3. The following code is intended to print (x,y) pairs for the function y=x2 between x=0 and x=10, in increments of 0.1. (It could be used to plot the function). What is wrong with the loop? What will happen if we run it as-is? How would you fix it? [4] 
    x = 0.0
while x != 10.0:
	y = x*x
	print "(%4.1f, %6.2f)" % (x, y)
	x += 0.1

    Due to inaccuracies in computer floating-point arithmetic, x will not equal 10.0 exactly, so the loop will continue past 10.0 forever (infinite loop). One quick fix is to change x != 10.0 to x <= 10.0.



  4. Name two operations/functions/properties that Python lists have that M2/C arrays do not. [4]
    • concatenation (+) (appending two lists),
    • repetition (*) (e.g., "Hi" * 3 == "HiHiHi"),
    • slice (extracting a sublist),
    • insert/delete



  5. What is a backtrace? [3]
    Shows the call stack: list of what functions are currently being evaluated







  6. Write "yes" or "no" next to each of the following six strings to indicate whether it can be used as a valid name for a user-defined Python variable. [6]
    true yes______ MODULE yes______ return no (reserved)______
    10thAnniversary no (starts with digit)______ www.twu.ca no (punctuation)______ _____ yes______
    (the last string is all underscores)
  7. Use the Python range() function to create this list: [ 11, 8, 5, 2 ]. [3]
    range(11,-1,-3)


  8. Evaluate each of the following Python expressions exactly as given, or if it produces an error, describe the error. Assume each expression is independent of the others. Assume all necessary imports have been done. For all expressions, assume the following initialization:[12] 
    	myApple = "Braeburn"
    1. 2.0 + 14 / 4 5.0
    2. 2 + 3>4 and (5/0 < 1) ZeroDivisionError
    3. "%03d%s" % (27.95, 'apples') '027apples'
    4. "%05.2f" % 3.1415926 '03.14'
    5. len(myApple) = 7 SyntaxError: can't assign
    6. range(len(myApple)) [0, 1, 2, 3, 4, 5, 6, 7]
    7. string.upper(myApple[1]) 'R'
    8. myApple[2:5] 'aeb'
    9. myApple < "Brayburn" True
    10. ord('z') - ord('w') 3
    11. 'z' - 'w' TypeError: can't subtract string
    12. 'z' + 'w' 'zw'



  9. The transcendental number e, the base of the natural logarithm, is approximately 2.718281828459045... and can be written as the infinite sum: 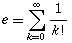where k! is k-factorial, or k(k-1)(k-2)....(3)(2)(1). Write a Python function e_sum() to calculate the partial sum. A parameter should be used to tell the function the maximum value of k to use in the sum. For example, e_sum(3) should add terms up to and including k==3. [8]

    Docstrings and comments are not required on this exam, however if your code is incorrect, your comments may earn you partial credit if they show good design thinking. Little partial credit will be given for uncommented incorrect code.
    See separate Python file e_sum.py.