(answers in web view)

Name:	_______________________________
Student ID:	_______________________________

Please show all your work! Total points: 100

1. For all values of a, find all solutions of the system below: [8]
   x + ay - z = 1
   -x + (a-2)y + z = -1
   2x + 2y + (a-2)z = 1
   For a=0: no solutions.
   For a=1: infinitely many solutions along a line (-t, t, -1).
   All other a: one solution, (1 - 1/a, 0, -1/a).
2. Find the equation of the plane containing the lines
   (x,y,z) = (1,-1,2) + (1,0,1)t and (x,y,z) = (0,0,2) + (1,-1,0)t. [6]
   x + y - z + 2 = 0
3. Let X be an arbitrary 2x2 matrix. Let W_X ⊆ M₂₂ be the set of all 2x2 matrices A such that AX = 0. Is W_X a subspace of M₂₂? Why or why not? [6]
   Closure under addition: If AX=0 and BX=0, then (A+B)X = 0.
   Closure under scalar mult: If AX=0, then (kA)X = 0.
   Yes, W_X is a subspace of M₂₂.
4. We learned two methods of polynomial interpolation: Vandermonde and Newton. A third method uses Lagrange polynomials: Given a set of points (x₀,y₀), ..., (x_n,y_n) with distinct x-values, define n+1 Lagrange polynomials as:
   L_i(x) = (x-x₀)(x-x₁) ... (x-x_i-1)(x-x_i+1) ... (x-x_n) / (x_i-x₀)(x_i-x₁) ... (x_i-x_i-1)(x_i-x_i+1) ... (x_i-x_n).
   (Note that the numerator is a polynomial of degree n, and the denominator is a scalar.) Observe that L_i(x_j) equals 0 if i≠j and equals 1 if i=j. Hence the polynomial p(x) that interpolates through the points can be built as
   p(x) = y₀L₀(x) + ... + y_nL_n(x).
   Consider a dataset (0,-1), (1, 1), (2, 0), (3, 2).
   1. Calculate the four Lagrange polynomials and derive the interpolating polynomial (and simplify). Double-check that the polynomial interpolates the points. [6]
      L₀(x) = (-1/6)(x-1)(x-2)(x-3)
      L₁(x) = (1/2)x(x-2)(x-3)
      L₂(x) = (-1/2)x(x-1)(x-3)
      L₃(x) = (1/6)x(x-1)(x-2)
      p(x) = (1/6)(x-1)(x-2)(x-3) + (1/2)x(x-2)(x-3) + (1/3)x(x-1)(x-2)
      = x³ - (9/2)x² + (11/2)x - 1.
   2. Re-derive the interpolating polynomial using either the Vandermonde or Newton method and verify that the result is the same. [6]
      Vandermonde matrix is

      1	0	0	0
      1	1	1	1
      1	2	4	8
      1	3	9	27

      Newton matrix is

      1	0	0	0
      1	1	0	0
      1	2	2	0
      1	3	6	6

   3. Compare the computational efficiency of these three methods for interpolating polynomials: Vandermonde, Newton, and Lagrange. Which is most efficient for finding a closed-form expression of the interpolating polynomial? Which is most efficient for evaluating the interpolant somewhere between data points? [4]
      Lagrange is quick and easy for getting a closed-form result -- although it takes some more work to simplify the expression. It is equivalent in efficiency to the Newton method -- relatively easy to compute a result, but requires additional work to simplify into standard form.
   4. Find the line which best fits these points using least-squares approximation. [4]
      The A matrix is

      1	0
      1	1
      1	2
      1	3

      Finding the normal system, A^TA is the 2x2 matrix [ [ 4, 6 ] [ 6, 14 ] ]. Similarly, A^Tb is (2, 7). Solving the normal system, (c₀, c₁) = (-7/10, 4/5). The line is y = (4/5)x - (7/10).
   5. What is the error in this approximation? (i.e., ||Ax-b||). [2]
      Ax = (3/10, -9/10, 9/10, -3/10), so ||Ax-b|| = 3√5/5 ≈ 1.34
   6. Find the quadratic (parabola) which best fits these points using least-squares approximation. [6]
      The A matrix is

      1	0	0
      1	1	1
      1	2	4
      1	3	9

      Finding the normal system, A^TA is the 3x3 matrix

      4	6	14
      6	14	36
      14	36	98

      Similarly, A^Tb is (2, 7, 19). Solving the normal system, (c₀, c₁, c₂) = (-7/10, 4/5, 0). The parabola is y = (4/5)x - (7/10); i.e., in this case, adding the x² term does not change the approximation.
   7. What is the error in this approximation? [2]
      Same as before
5. Consider the linear transform from ℜ⁵ to ℜ⁴ whose standard matrix A is given below:

   3	5	5	2	0
   1	0	2	2	1
   1	1	1	-2	-2
   -2	0	-4	-4	-2

   1. Compute the rank of the matrix A. [4]
      Reduce to:

      1	0	0	-6	-5
      0	1	0	0	0
      0	0	1	4	3
      0	0	0	0	0

      Rank = 3.
   2. Are the rows of A linearly independent? If not, find a subset which is linearly independent, and express the other rows as linear combinations of that subset. [4]
      Rowspace: rows 1, 2, 3 are linearly independent.
   3. The transform maps a whole subspace of ℜ⁵ onto 0. Find a basis for that subspace. [4]
      Nullspace: (6,0,-4,1,0) and (5,0,-3,0,1).
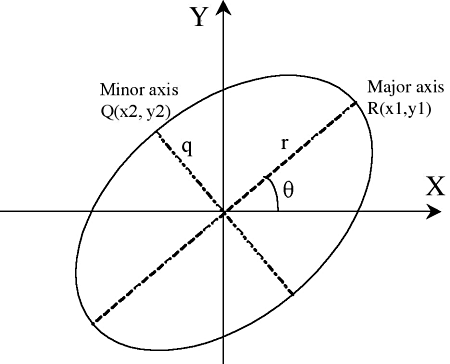6. Define an inner product on ℜ² such that the unit circle under your inner product is an ellipse with major axis of half-length r=10 and minor axis of half-length q=6, tilted at an angle of θ=π/6: [6]
   Without the rotation, the inner product <(x₁, y₁), (x₂, y₂)> = (1/100)x₁x₂ + (1/36)y₁y₂ would produce the right ellipse. This is the inner product generated by the transform matrix corresponding to contraction by 1/10 in x and 1/6 in y; i.e., shrinking the ellipse back down to the regular Euclidean unit circle.
   Extending this idea, the inner product we want is generated by the matrix which transforms the given ellipse back down to the Euclidean unit circle: first rotation clockwise by π/6, then contraction by 1/10 in x and 1/6 in y. We can assemble this matrix as the product:
   

   1/10	0
   0	1/6

   *

   √3/2	1/2
   1/2	√3/2

   =

   √3/20	1/20
   -1/12	√3/12

   
   This matrix takes (x,y) and transforms it to ( (√3/20)x + (1/20)y, -(1/12)x + (√3/12)y ).
   The corresponding inner product is <(x₁, y₁), (x₂, y₂)> = (3/400 + 1/144)x₁x₂ + (√3/400 - √3/144) ( x₁y₂ + x₂y₁ ) + (1/400 + 3/144)y₁y₂.
   
7. Consider C[0,2π] with the inner product <f,g> = ∫₀^2π f(x)g(x)dx.
   Let u₀(x)=1, u₁(x)=cos(x), u₂(x)=cos(2x), ..., u_n(x)=cos(nx),
   and u_n+1(x)=sin(x), u_n+2(x)=sin(2x), ..., u_2n(x)=sin(nx).
   The subspace of C[0,2π] spanned by all the u_i is called the set of trigonometric polynomials of order n.
   1. Show that {u₀, u₁, u₂} are linearly independent. [4]
      Wronskian:

      1	cos(x)	cos(2x)
      0	-sin(x)	-2sin(2x)
      0	-cos(x)	-4cos(2x)

      The determinant is 4sin(x)cos(2x) - 2sin(2x)cos(x), which is not identically zero, so the three functions are linearly independent.
   2. It can be shown (you may assume) that indeed all the u_i are linearly independent, and hence form a basis for the trigonometric polynomials of order n. Convert them into an orthonormal basis. [10]
      Some trig identities you may find helpful:
      cos(α)cos(β) = (1/2)cos(α-β) + (1/2)cos(α+β)
      ⇒ cos²(α) = (1/2) + (1/2)cos(2α), and
      sin(α)sin(β) = (1/2)cos(α-β) - (1/2)cos(α+β)
      ⇒ sin²(α) = (1/2) - (1/2)cos(2α).
      Also, sin(α)cos(β) = (1/2)sin(α-β) - (1/2)sin(α+β).
      It turns out that the u_i are already orthogonal, so we just need to normalize them. ||u₀|| = √(2π), and the rest all have norm √π.
      The textbook covers Fourier series in more detail; see section 9.4, p.474.
   3. The function f(x) = x is not a trigonometric polynomial. Find the trigonometric polynomial of order n that best approximates f(x) (least squares). (This is the Fourier series of f(x).) [6]
      Approximate solution is the projection onto the space of trig polys, which can be obtained via inner products with the orthonormal basis. The inner product with u₀=1/√(2π) is π√(2π). The others can be obtained via ntegration by parts: all the inner products with cos are zero, and the inner product with (1/√π)sin(kx) is -2√π/k.
      So the approximate solution is f(x) = x ≈ π - 2( sin(x) + sin(2x)/2 + sin(3x)/3 + ... + sin(nx)/n ).
8. For the matrix A given below, find Aⁿ for any positive integer n: [12]

   8	7	7
   -5	-6	-9
   5	7	10

   
   λ=1: (1,-2,1)
   λ=3: (0,1,-1)
   λ=8: (1,-1,1)
   Aⁿ = PDⁿP^-1:
   

   1	0	1
   -2	1	-1
   1	-1	1

   *

   1	0	0
   0	3n	0
   0	0	8n

   *

   0	-1	-1
   1	0	-1
   1	1	1

   
   The final closed-form solution for Aⁿ is
   

   8n	-1 + 8n	-1 + 8n
   3n - 8n	2 + 8n	2 - 3n - 8n
   - 3n + 8n	-1 + 8n	-1 +3n + 8n